1. 베이즈 정리(Bayes' Theorem)

 

 

 

<베이즈 정리>

베이지안 방법론에 대해 배우기 전에 베이즈 정리에 대해 알아보자.

베이즈 정리는 다음과 같이 정리된다. 

 

 

 

베이즈 정리가 무엇을 의미하는 지 알기 위해 아랫쪽에 있었던 공식을 자세히 살펴보자.

E를 "새롭게 관측해 얻은 값(정보)", A를 "알아내고 싶은 값(정보)"로 생각한다면,

P(A|E)는 "새롭게 관측해 얻은 값들을 반영한, 내가 알고 싶은 정보"가 되는 것이다.

베이즈 정리는 새로운 관측값으로 생긴 변화를 확률 계산 시 반영하는 법을 알려주는 식이다.

 

 

 

<사전확률과 사후확률>

베이즈 정리에서 등장하는 사전확률, 사후확률이라는 용어에 대해 알아보자.

사전확률(prior probability)는 관측자가 관측 전 가지고 있는 확률분포로, 위 경우에는 P(A)이다. 즉, 새로 관측해 알아낸 값인 E로 업데이트하기 전의 확률이다. 

사후확률(posterior probability)는 정보로 사전 확률을 업데이트 한 결과로 발생하는 조건부확률을 의미한다. 위 경우에서는 P(A|E)이다. 

 

 

 

아래 예제를 통해 베이즈 정리를 이해해보자. 

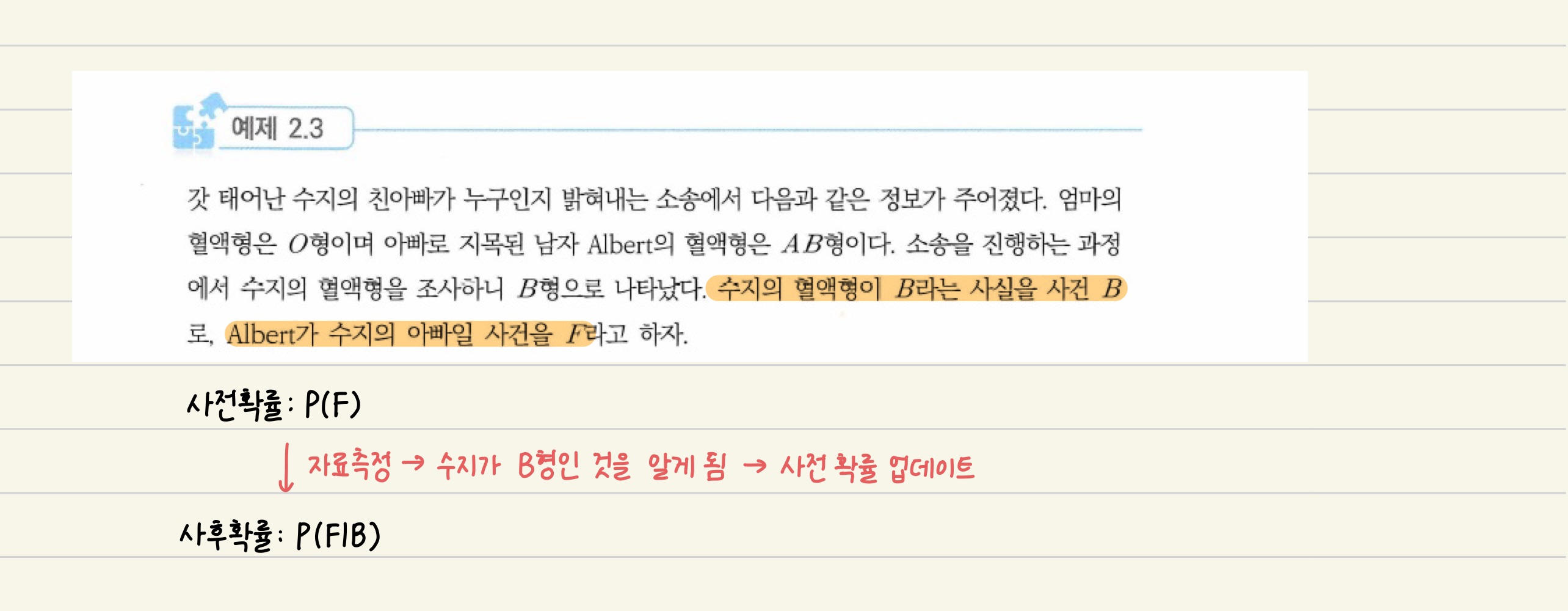
Albert가 수지의 아빠일 사건을 F라고 한다면, 수지의 엄마와 Albert와의 관계, 주변 사람들의 증언 등에 의하여 Albert가 수지의 아빠일 가능성 P(F)를 추측할 수 있을 것이다. 이때 P(F)는 자료, 즉 혈액형을 측정하기 이전의 확률이므로 사전 확률이다.

반면 혈액형 조사 이후의 확률은 B라는 사건을 반영한 확률이므로 P(F|B)로 나타낼 수 있고, 이는 사후 확률이다. 

 

 

 

<베이즈 정리를 이용한 문제풀이>

베이즈 정리를 이용해 문제에서 요구하는 확률을 구해보자. 

 

 

 

 

 

<참고 - 확률분포>

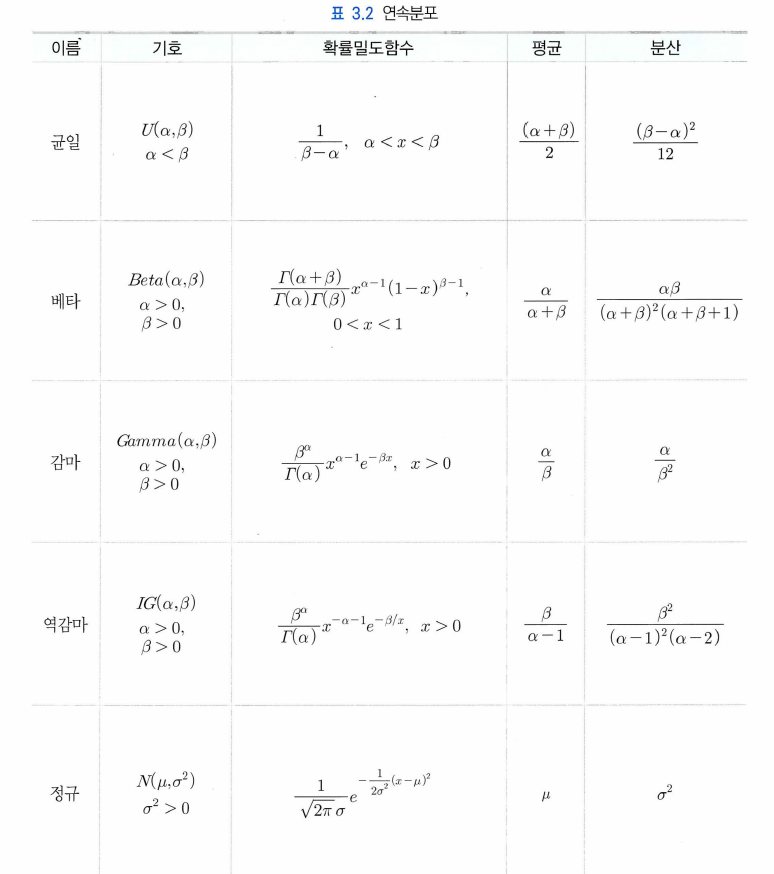
앞으로 베이지안 방법론에서 자주 보게 될 확률분포는 다음과 같다. 
특히 손으로 직접 계산할 때는 확률함수의 식을 잘 봐두는 것이 중요하다. 

 

 

 

확률함수를 처음 본다면 아래 카테고리 글들을 확인하면 된다. 

https://portrait-of-youngblood.tistory.com/40

3. 이산확률변수 (Discrete Random Variables)