4. 단순선형회귀식의 진단 - 검정 (Diagnostics for a Simple Linear Model Using Test)
단순선형회귀식의 정의와 기본적인 가정에 따르면, 회귀 모형은 몇가지 조건을 만족해야 한다.
이번 단원에서는 통계적 검정을 이용한 단순선형회귀식을 진단에 대해 다룰 예정이다.
1. Brown-Forsythe 검정
Brown-Forsythe 검정은 오차항이 상수분산(등분산)을 갖는지 알아볼 수 있는 검정이다.
X 값이 작은 그룹과 큰 그룹으로 나누어 둘의 분산을 구하고, 두 분산을 비교해 분산값이 크게 다르지 않은지 검정하는 과정을 거친다.

데이터를 이용해 직접 R에서 검정을 이용한 진단을 해보자.
Toluca Company의 데이터에 대하여 Brown-Forsythe 검정을 사용해 오차분산이 X의 수준에 따라 달라지는지를 판단하고 싶을 때, 아래와 같은 코드를 사용할 수 있다.
#데이터 불러오기
Toluca <- read.table(file="C:/Temp/Toluca.txt")
names(Toluca) <- c("X","Y")
#X값의 크기순으로 데이터 정렬
ord <- order(Toluca$X)
Toluca <- Toluca[ord,]
attach(Toluca)
#회귀 모형 만들기, 잔차 구하기
model_Tc <- lm(Y~X, data=Toluca)
resid <- model_Tc$residuals
median(Toluca$X) #중앙값이 70임을 확인
#그룹1과 그룹2의 절대 편차 구하기
d1 <- abs(resid[Toluca$X<=70]-median(resid[Toluca$X<=70]))
d2 <- abs(resid[Toluca$X>70]-median(resid[Toluca$X>70]))
#두 그룹의 분산에 대한 t-test 실행하기
t.test(d1,d2, var.equal = TRUE)
<결과분석>

p-value가 0.201이므로 유의수준 0.05에서 가설을 기각할 수 없다.
따라서 주어진 모형은 오차항의 분산이 상수이다. (등분산성을 만족한다.)
2. Breusch-Pagan 검정
Breusch-Pagan 검정 또한 Brown-Forsythe 검정처럼 오차항이 상수분산(등분산)을 갖는지 알아볼 수 있는 검정이다.
이 검정은 오차항의 분산을 r0 + r1 x X로 두고, r1=0일 때 상수값을 갖는다는 관계를 이용한 검정이다.
자유도가 1인 카이제곱 검정통계량을 이용해 검정할 수 있다.

<방법1>- ncvTest 함수 사용
#데이터 불러오기는 생략함
#패키지 설치, 로딩
install.packages("car")
library(car)
#Breusch-Pagan 검정
ncvTest(model_Tc)
#유의수준 0.05에서의 카이제곱 기각역 (critical value) 구하기
qchisq(0.95, 1)
<결과분석>


<방법2> - 기술통계량 직접 계산
resid <- model_Tc$residuals
resid.sq <- resid**2
model_sq <- lm(resid.sq~X, data=Toluca)
anova(model_sq)
anova(model_Tc)


방법1에서 구한 검정통계량과 직접 계산한 값이 일치함을 알 수 있다.
3. 적합성 결여 검정 (Lack of Fit Test)
적합성 결여 검정(Lack of Fit Test)는 선형회귀함수가 주어진 자료를 설명하기에 적합한지를 확인하는 검정이다.
적합성 결여 검정을 하기 위해서는 완전 모형(full model)과 축소 모형(reduced model)에 대해 먼저 알아야 한다.



데이터를 이용해 직접 R에서 검정을 이용한 진단을 해보자.
주어진 데이터에서 I는 반복관측값의 개수, X는 예측 변수, Y는 반응 변수이다.
#데이터 불러오기
data3 <- read.table(file="C:/Temp/DataSet.txt")
names(data3) <- c("I","X","Y")
#자료 시각화
with(plot(X,Y), data=data3)
lines(data3$X, reduced$fitted, col=3, lwd=2)
with(lines(X, mean, col=2, lwd=2), data=new)
<그래프>
빨간색 그래프는 y의 평균값을 연결한 그래프이고, 초록색 그래프는 회귀 모형이다.
두 그래프 사이에 차이가 있음을 알 수 있고, 적합성 결여 검정 (lack of fit test)가 필요함을 알 수 있다.

<방법1>- reduced model과 full model의 ANOVA 사용
# 적합성 결여 검정
new <- data.frame(mean=with(tapply(Y,factor(X),mean),data=data3))
new <- data.frame(X=as.numeric(row.names(new)),new)
full <- lm(Y~factor(X), data=data3)
reduced <- lm(Y~X, data=data3)
anova(reduced,full)
p-value가 0.005894이므로 유의수준 0.05에서 가설을 기각할 수 있다.
따라서 주어진 모형은 적합하지 않은 모형이다.
<방법2> - 기술통계량 직접 계산
anova(reduced)
anova(full)
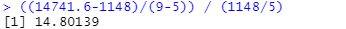
방법 1과 같은 결괏값을 얻을 수 있다.