1. 단층 퍼셉트론(Single-Layer Perceptron)
1. 퍼셉트론(perceptron)의 개념
퍼셉트론은 인공신경망(딥러닝)의 기원이 되는 알고리즘이다.
퍼셉트론은 다수의 신호를 입력(input)으로 받아 0 혹은 1을 신호로 출력(output)한다.
아래 그림은 입력으로 2개의 신호를 받은 퍼셉트론의 예시이다. x1, x2는 입력 신호, y는 출력 신호, w1과 w2는 가중치이다. 왼쪽의 원은 뉴런(neuron) 혹은 노드(node)라고 부른다. 입력 신호가 뉴런에 보내질 때 각각 고유한 가중치가 곱해지고 (w1x1, w2x2), 뉴런에서 보내온 신호의 총합(w1x1+w2x2)이 정해진 값을 넘어설 때 1을 출력한다. 이 때 정해진 값을 임계값이라 하고, θ로 나타낸다.

수식과 그림으로 퍼셉트론을 표현하면 다음과 같다.
(가중치는 각 신호가 결과에 주는 영향력을 조절하는 요소로 작용한다. 가중치가 클수록 해당 신호가 더 중요함을 뜻한다.)

임계값인 θ를 좌변으로 이항하면, -θ는 편향(bias)를 의미하게 된다.

2. 논리연산자와 퍼셉트론
간단한 논리연산자 예제를 통해 퍼셉트론을 살펴보자.
먼저 AND 게이트를 퍼셉트론을 이용해 구현하는 문제를 풀어보자. AND 게이트는 이진법을 이용한 불 연산(boolean expression)을 사용한다. 입력 신호는 0 혹은 1이고, 입력 신호가 같을 때는 1을 출력하고 입력 신호가 다를 때는 0을 출력해야 한다. 입력 신호와 출력 신호의 진리표는 다음과 같다.

이 AND 게이트를 퍼셉트론으로 표현하려면 노드의 개수, 가충치, 임계값을 정하면 된다.
1. 입력 신호를 받아들이는 노드 결정 -> 두 개 (0 or 1)
2. 출력 신호를 받아들이는 노드 결정 -> 한 개 (한 개의 답을 출력함)
3. w1, w2, θ의 값 결정 -> ??
퍼셉트론으로 구현해야 하는 값을 그래프로 표현하면 다음과 같다.

먼저 가중치를 정하자.
이 논리 연산에서는 X1과 X2가 각각 출력값에 미치는 중요도가 같다. (같은 영향을 미친다.) 따라서 가중치는 w1=1, w2=1로 설정하자. 이 값을 경계가 되는 식 w1x1+w2x2-θ=0에 대입하면 x1+x2-θ=0이 된다.
다음으로 우리가 해야할 일은 값을 잘 구분할 수 있는 경계선 x1+x2-θ=0 의 θ 값을 잘 정해주는 것이다. θ 만 잘 결정해준다면 직선이 0과 1 사이에 잘 그어진다. (이때 출력되는 값을 구분해주는 θ 의 값은 유일하지 않기 때문에, 이를 만족시키는 경계선은 한 개가 아니다.)
AND 게이트의 조건을 만족시키는 가중치, 임계값의 예시를 살펴보자.
아래와 같이 설정된다면 입력값 x1과 x2 모두가 1일 때만 가중 신호의 총합이 임계값보다 커지게 되어, 경계선 한 개로 출력값이 잘 구분된다. 이때 (w1, w2, θ )가 될 수 있는 값은 (0.5,0.5,0.7), (0.5,0.5,0.8), (1.0,1.0,1.0) 등 다양하다.

이처럼 가중치와 임계값을 직접 설정해 AND 연산을 퍼셉트론에서 구현해보았다. 이번에는 NAND(Not AND) 게이트를 퍼셉트론으로 구현하자.
NAND 게이트는 두 값이 모두 1일 때만 0을 출력하고, 그 외에는 1을 출력한다. NAND 게이트를 퍼셉트론으로 구현하기 위해 가중치와 임계값을 정해야 한다.

퍼셉트론으로 구현해야 하는 값을 그래프로 표현하면 다음과 같다.

AND 게이트와 값이 모두 반대이기 때문에 AND 게이트를 구현하는 매개변수(가중치, 임계값)의 부호를 모두 반전하면 NAND 게이트가 된다. 혹은 (w1, w2, θ) = (-0.5, -0.5, 0.7) 등 다른 조합을 찾을 수 있다.
OR 게이트 또한 퍼셉트론으로 구현할 수 있다.
OR 게이트는 입력 신호 중 하나 이상이 1이면 출력이 1이 되는 논리 회로이다.
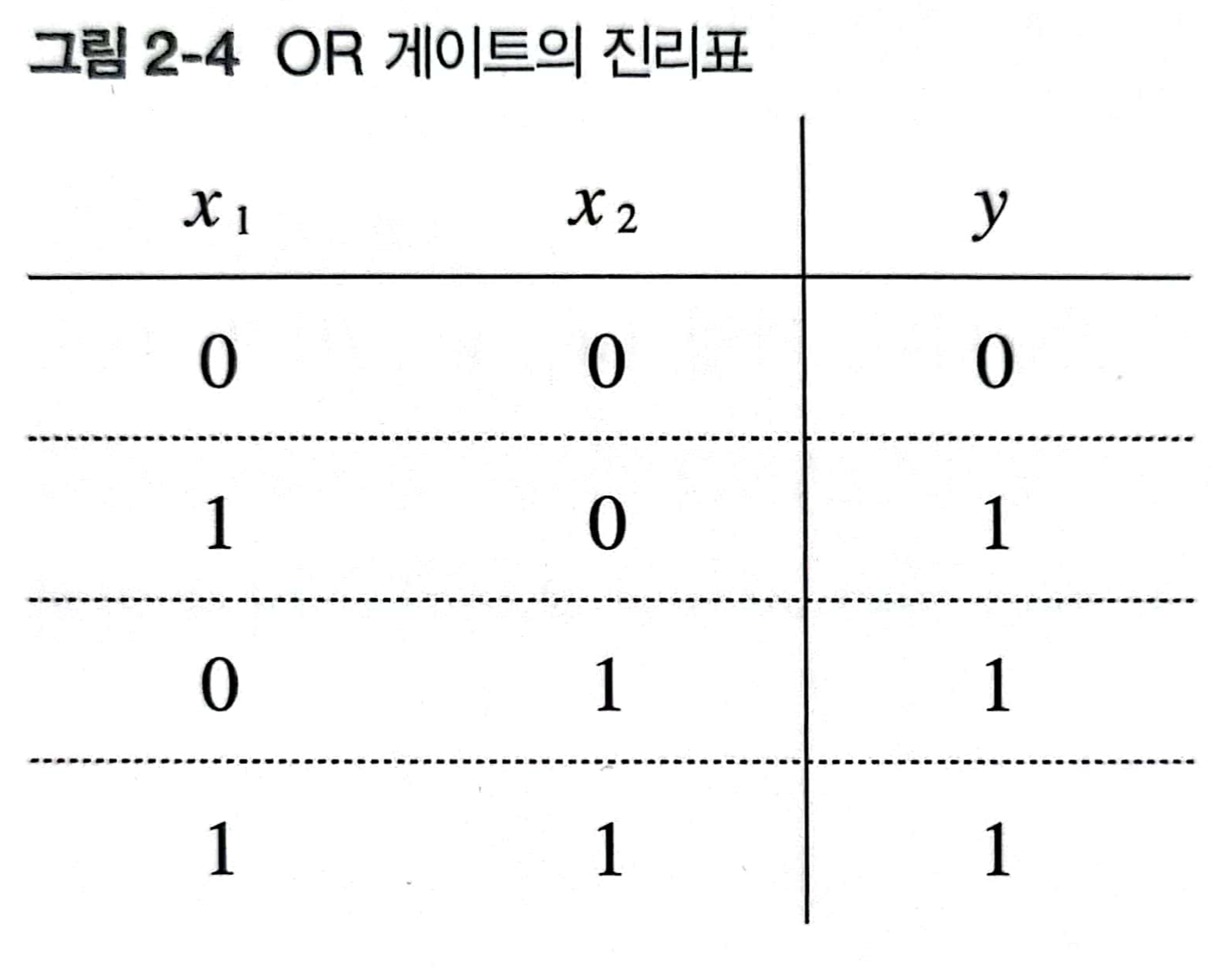

이를 만족하는 값에는 (w1, w2, θ) = (1, 1, -0.5)가 있다.
<결론>
이와 같이 퍼셉트론으로 AND, NAND, OR 논리 회로를 표현할 수 있음을 알았다. 여기서 중요한 점은 퍼셉트론의 구조가 AND, NAND, OR 게이트 모두에서 똑같다는 것이다. 세 가지 게이트에서 다른 것은 매개변수(가중치와 임계값)의 값 뿐이다. 즉, 똑같은 구조의 퍼셉트론을 매개변수의 값만 잘 조정해주면 모든 논리 회로를 표현할 수 있는 것이다.
3. 파이썬에서 퍼셉트론 구현하기
AND 논리 회로를 파이썬으로 구현하자. x1과 x2를 인수로 받아 값을 출력하는 AND 함수를 다음과 같이 구현할 수 있다.
|
1
2
3
4
5
6
7
8
9
10
|
def AND(x1,x2):
w1,w2,theta = 1,1,1.5
value = x1*w1 + x2*w2
if value <= theta:
return 0
elif value > theta:
return 1
print(AND(0,0),AND(1,0),AND(0,1),AND(1,1))
## 0 0 0 1
|
cs |
혹은 numpy 패키지를 이용해 다음과 같이 구현할 수 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
import numpy as np
def AND(x1, x2):
X = np.array([1, x1, x2])
W = np.array([-1.5, 1, 1])
if np.dot(X, W) <= 0: # np.dot(X, W.T) = np.sum(X*W)
return 0
else:
return 1
for x in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = AND(x[0], x[1])
print("AND", x, " = ", y)
## AND (0, 0) = 0
## AND (1, 0) = 0
## AND (0, 1) = 0
## AND (1, 1) = 1
|
cs |
'