신경망 학습의 목적은 손실 함수의 값을 가능한 한 낮추는 매개변수를 찾는 것이다.
이는 곧 학습을 통해 매개변수의 최적값을 찾는 문제이며, 이러한 문제를 푸는 것을 "최적화(optimization)"라고 한다.
신경망의 특징은 데이터를 보고 학습할 수 있다는 점이다. 데이터에서 학습한다는 것은 가중치 매개변수의 값을 데이터로 보고 자동으로 결정하는 것이다. (실제 신경망에서는 매개변수가 수천에서 수만개이고, 딥러닝에서는 그 수가 수억에 이를 수 있다. 모든 매개변수를 수작업으로 결정하는 것이 불가능하기 때문에 자동으로 결정되어야 한다.)
※ 손실 함수
손실 함수는 신경망 성능의 '나쁨'을 나타내는 지표로, 현재의 신경망이 훈련 데이터를 얼마나 잘 처리하지 '못'하느냐를 나타낸다.
신경망은 학습에서 손실함수 값을 기준으로 최적의 매개변수 값을 탐색한다. 대표적인 손실함수에는 평균오차제곱(Mean Square Error, MSE)이 있다.

1. 최적화 = 손실 함수의 미분
신경망 학습에서는 최적의 매개변수(가중치와 편향)을 탐색할 때 손실 함수의 값을 가능한 한 작게 하는 매개변수의 값을 찾는다.
매개변수의 미분 (기울기)을 계산하고, 그 미분 값을 단서로 매개변수의 값을 서서히 갱신하는 과정을 반복한다. 이때 가중치 매개변수의 손실 함수 미분이란 '가중치 매개변수의 값을 아주 조금 변화시켰을 때, 손실 함수가 어떻게 변하나'라는 의미이다.
2. 일변수 함수의 미분
파이썬에서의 미분과 우리가 직접 함수를 미분하는 계산은 다르다.
아래 식처럼 직접 미분값을 구하는 계산을 해석적 미분이라고 한다.
우리가 수학 시간에 배워왔던 미분 방식이다.
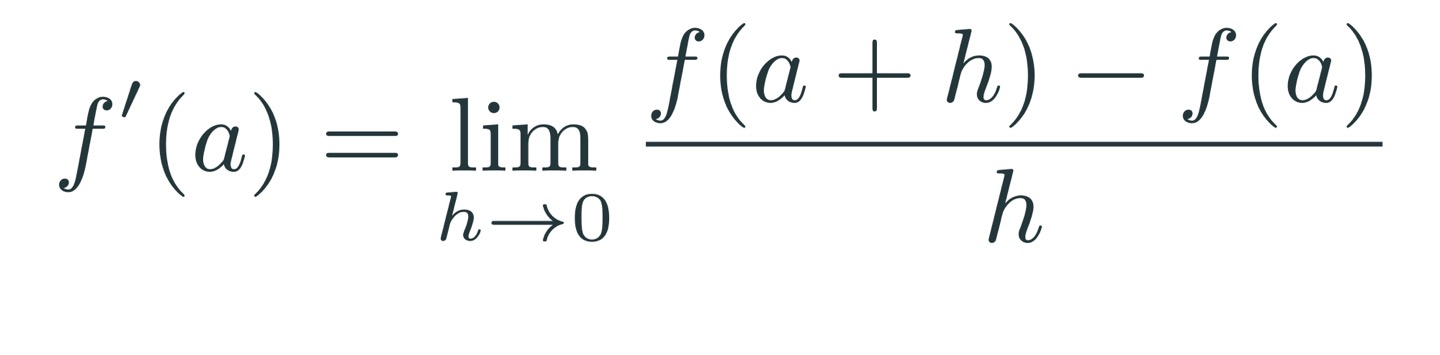
파이썬에서 연속값을 처리하는 것이 불가능하기 때문에 직접적으로 미분값을 계산하지 않고, 아래 식처럼 근사시킨 미분값을 구해야 한다.
이처럼 아주 작은 차분(임의 두 점에서의 함수 값들의 차이)으로 미분하는 것을 수치 미분이라고 한다.
아래 식처럼 (x+h)와 x의 함숫값 차이를 이용하는 것을 전방 차분(forward finite difference)이라고 한다.

하지만 수치 미분에는 오차가 포함되기 때문에 Taylor Expansion(테일러 급수)를 이용해 이 오차를 줄이기도 한다.
테일러 급수를 이용한 수치 미분 식은 다음과 같다.
아래 식처럼 (x+h)와 (x-h)의 함숫값 차이를 이용하는 것을 중심 차분(central finite difference)이라고 한다.

(참고) a+h와 a-h의 차분을 이용한 식의 값이 a+h와 a의 차분을 이용한 식의 값보다 정확한 이유는 다음과 같다.
아래와 같은 테일러 급수 식을 이용하면


중심 차분을 이용해 수치 미분 계산을 했을 때 실제 미분값과의 오차가 더 작게 계산된다는 것을 알 수 있다.
3. 파이썬에서의 수치미분
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
#전방 차분을 이용해 미분값 출력하는 함수 만들기
def numerical_diff(f,x,h=1e-6):
return (f(x+h)-f(x))/h
#중심 차분을 이용해 미분값 출력하는 함수 만들기
def numerical_diff2(f,x,h=1e-6):
return (f(x+h)-f(x-h))/(2*h)
#미분할 함수 f1 임의로 생성하기
f1=lambda x : x**2
print(numerical_diff(f1,1))
print(numerical_diff2(f1,1))
## 2.000000000002
## 2.000000000002
|
cs |
주의: h값에 너무 작은 수를 대입하면 0에 가까운 수가 아닌 0으로 취급해서 에러가 발생함
4. 경사하강법을 이용한 최소화
기울기를 이용해 손실 함수의 최솟값을 찾는 것이 경사법이다. 주의할 점은, 함수의 값을 낮추는 방안을 제시하는 지표가 기울기인 것은 맞지만 기울기가 가리키는 곳에 정말 함수의 최솟값이 있는지, 즉 그쪽이 정말로 나아가야할 방항인지는 보장할 수 없다는 점이다. 기울어진 방향이 꼭 최솟값을 가리키는 것은 아니지만, 함수가 기울어진 방향으로 가야 함수의 값을 줄일 수 있다. 따라서 최솟값이 되는 지점을 찾는 문제에서는 기울기 정보를 단서로 나아갈 방향을 정해야 한다.
경사법은 현 위치에서 기울어진 방향으로 일정 거리만큼 이동한다. 그 다음 이동한 곳에서도 마찬가지로 기울기를 구하고, 또 기울어진 방향으로 나아가기를 반복해 함수의 값을 점차 줄여나간다. 경사법은 기계학습의 최적화에서 흔히 쓰는 방법이고, 신경망 학습에서는 경사법을 많이 사용한다. 경사법으로 최솟값을 찾는 방법을 경사 하강법(gradient descent method), 최댓값을 찾는 방법을 경사 상승법(gradient ascent method)라고 한다.

먼저, 랜덤한 위치(x0,f(x0))에서 시작하고, 위치한 곳에서의 미분값으로 접선의 기울기를 파악한다. 미분값의 반대 방향으로 움직여 경사가 반대인 방향(경사가 줄어드는 방향)으로 움직이고, 이 과정을 반복한다.

5. 파이썬에서의 경사하강법 구현
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
#수치미분 함수 미리 정의하기
def numerical_diff2(f,x,h=1e-6):
return (f(x+h)-f(x-h))/(2*h)
#변수 설명: 최솟값을 찾아야 하는 손실함수를 func, 초기 위치를 init_x, 학습률을 lr, 계산 반복횟수를 iteration이라고 설정
def gradient_descent(func, init_x, lr=0.1, iteration=100):
x=init_x
for i in range(iteration):
grad=numerical_diff2(func,x)
x -= lr*grad
return x
#예시로 넣을 이차함수 f1 정의
f1=lambda x : x**2
#120이라는 점에서 시작해 f1 함수가 최댓값을 갖는 지점을 경사하강법으로 찾음
gradient_descent(f1, 120)
##[출력] 2.4444431763105418e-08
|
cs |
경사하강법으로 최솟값을 가질 때의 x값은 0임을 알 수 있다.
'인공지능∙모델링 > 딥러닝' 카테고리의 다른 글
| 6. 딥러닝에서 과적합(Overfitting)을 막는 방법 (0) | 2023.12.12 |
|---|---|
| 5. 인공신경망의 학습 (Neural Network Training) (0) | 2023.12.12 |
| 3. 인공 신경망(Artificial Neural Network, ANN) (0) | 2023.10.08 |
| 2. 다층 퍼셉트론(Multi-Layer Perceptron) (0) | 2023.10.06 |
| 1. 단층 퍼셉트론(Single-Layer Perceptron) (0) | 2023.09.20 |





댓글