1. 사후 분포 계산하기
이전까지 사전분포에 새로 얻게 된 정보를 결합해 사후분포를 추정하는 베이지안 방법을 살펴보았다.
앞에서 배웠던 예시를 아래 예제에 적용해보자.
베르누이-균일 모델(Bernoulli-Uniform random effect model)
아래의 새로운 교육방법이 효과가 있는지 알아보기 위해 40명의 어린이들을 표본으로 삼아 조사한 사례이다.
변수 Xi를 i번째 어린이에게 효과가 있으면 1, 아니면 0 값을 갖는다고 정의하고, Xi는 베르누이 분포를 따른다고 볼 수 있다.
총 15명에게 효과가 있고, 25명에게는 효과가 없다는 결과가 나왔고, 이 정보를 새롭게 반영해 사후 분포를 구하면 된다.

결론적으로 사전 분포가 균일 분포, 관측치가 베르누이 분포를 따를 때 사후 분포는 베타 분포를 따른다는 것을 알 수 있다.
아래는 위에서 얻은 사후분포로 평균값, 분산, 중간값을 구하는 예제이다.
사후분포을 얻게 되어 좋은 점은, 업데이트한 확률분포(사후분포)로 평균값, 분산, 중앙값같은 대푯값들을 추출할 수 있다는 것이다.
특히 이 사례에는 사후분포가 특성이 알려진 베타분포를 따르기 때문에 많은 값들을 알아낼 수 있다.

베르누이-베타 모델 (Bernoulli-Beta random effect model)
위에서 사전분포와 관측치가 따르는 분포를 통해 사후 분포를 알아냈던 것처럼 아래 문제를 계산하자.
위에서 사용했던 균일분포는 Beta(1,1) 분포와 같으므로, 이를 확장해 일반적인 베타 분포도 베르누이분포와 결합했을 때 베타분포가 나온다는 것을 보일 수 있다.
아래와 같은 계산 과정을 통해 증명해보이자.

위에서 얻은 공식을 통해 사후 분포를 복잡한 계산 없이 간단하게 계산해보자.
1(성공)의 개수가 5개, 0(실패)의 개수가 5회인 관측치가 주어졌으므로 사후분포는
Beta(16+5, 26+5) = Beta(21, 31)을 따른다.

베르누이-베타 모델의 공식을 이용해 사후분포를 구하고 R에서 그래프로 표현해보자.
검은색 그래프가 사전확률분포, 빨간색 그래프가 새롭게 얻은 정보를 반영한 사후확률분포이다.
새로운 정보로 업데이트했을 때 확률분포가 달라진다는 것을 알 수 있다.
## R코드
x = seq(0, 1, 0.01) # 그래프에 나타낼 x값 설정
y_prior = dbeta(x, shape1=16, shape2=26) # 사전확률 설정 (베타 분포)
plot(x,y_prior,type="l") # 사전확률을 그래프로 표현하기
y_post = dbeta(x, shape1=21, shape2=31) # 사후확률 설정 (베타 분포)
points(x, y_post, type="l", col=2) # 사후확률을 그래프로 표현하기
2. 예측 분포 계산하기
앞에서는 관측치를 반영해 사전분포를 업데이트한 사후분포를 구했다.
이제는 사후분포를 바탕으로 새롭게 얻을 데이터 값 y를 예측해보자.
위에서 봤던 사전분포가 베타 분포, 관측치가 베르누이 분포, 사후분포가 베타 분포를 따를 때의 상황을 살펴보자.
구한 사후분포를 통해 새롭게 얻을 데이터 y(n+1)의 확률, 평균값, 분산을 구할 수 있다.

참고)
아래는 식을 전개할 때 쓰이는 double conditional expectation (이중 조건부확률 기댓값) 공식이다.
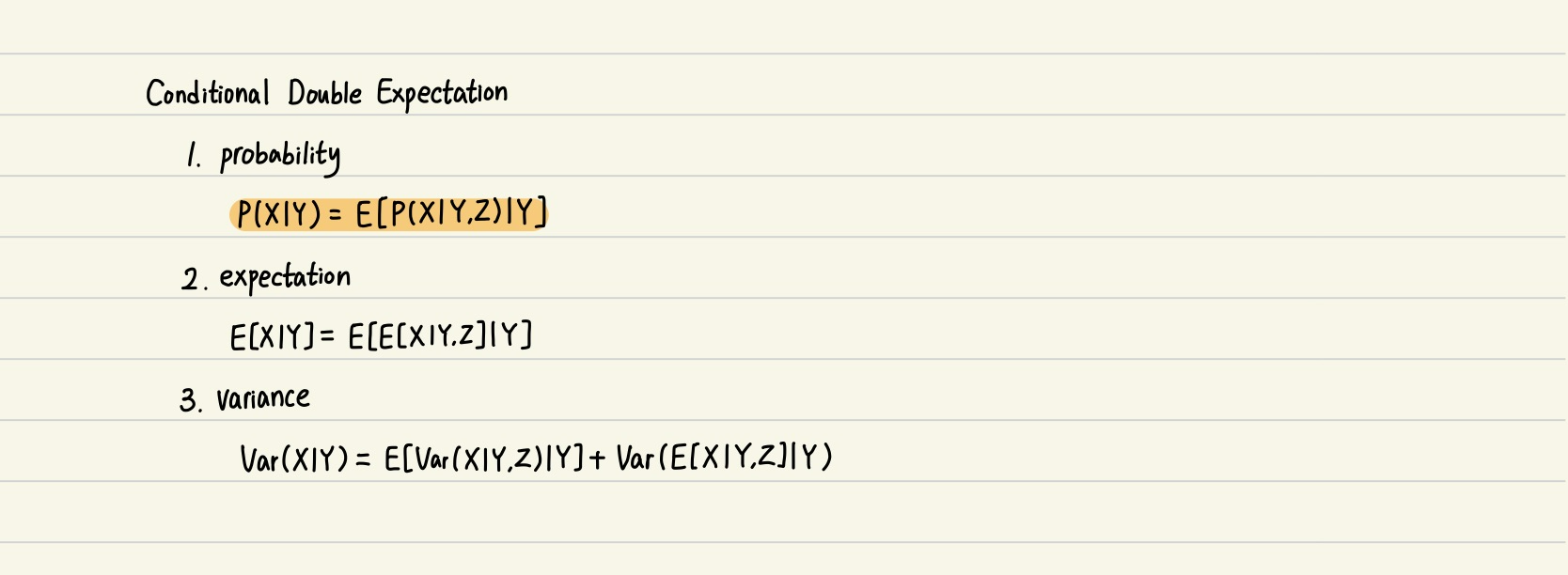
1, ... , 12번까지의 데이터를 알 때 13번째 데이터의 예측확률을 구하는 문제를 풀어보자.
(여기서는 사전분포에 관한 정보가 없으므로 사전분포를 Beta(1,1) = Unif(0,1)로 가정한다. )

<정리>
| 사전확률의 분포 | 관측치의 분포 | 사후확률의 분포 |
| 균일 분포 (uniform distribution) | 베르누이 분포 (Bernoulli distribution) | 베타 분포 (Beta distribution) |
| 베타 분포 (Beta distribution) | 베르누이 분포 (Bernoulli distribution) | 베터 분포 (Beta distribution) |
주의!) 균일분포는 Beta(1,1) 분포로 Beta 분포의 특수한 경우에 해당한다. 즉, 균일분포는 베타분포에 속하므로, 베르누이 분포와 결합되었을 때 베타 분포가 나올 수밖에 없는 것이다.
'심화통계학 > 베이지안 방법론' 카테고리의 다른 글
| 4. 포아송-감마 모델(Poisson-Gamma random effect model) (1) | 2024.04.13 |
|---|---|
| 2. 베이지안 추정(Bayesian Inference) (0) | 2024.04.10 |
| 1. 베이즈 정리(Bayes' Theorem) (0) | 2024.04.10 |




댓글