회귀 분석이란, 여러가지 변수 간의 관계성을 알아보는 통계학의 방법론이다.
즉, 변수 간 관계가 있는가? 음의 상관관계와 양의 상관관계 중 어떤 상관관계를 갖는가? 만을 분석할 수 있는 상관 분석 (Correlation analysis)과 달리 변수 간의 관계를 나타낼 수 있는 식을 세우고, 이를 바탕으로 값을 예측까지 할 수 있는 통계 분석, 추론 방법이다.
우리가 관심이 있는 변수를 Y로 두고, 변수 Y를 예측하는데 도움을 주는 변수를 x라 하자.
Y를 반응 변수 (response variable) 혹은 종속 변수 (dependent variable)로 부르고,
x를 예측 변수 (predictor variable), 혹은 독립 변수 (independent variable) 혹은 설명 변수 (explanatory variable)이라고 부른다.
(x를 회귀변수 (regressor variable)이라고 부르기도 한다. 후에 등장하는 회귀 계수 (parameter)와는 다르므로 주의하자.)

회귀 식은 주로 두 구성 요소로 이루어져있다.
변수 간의 관계적 경향을 나타내는 함수식 Y=f(x)와, 데이터의 현실적인 오차를 표현해주는 에러로 이루어진다.
실제로 Y=f(x)가 모든 데이터를 정확히 표현하지 못하는 한계가 있기 때문에, 에러를 도입한 것이다.
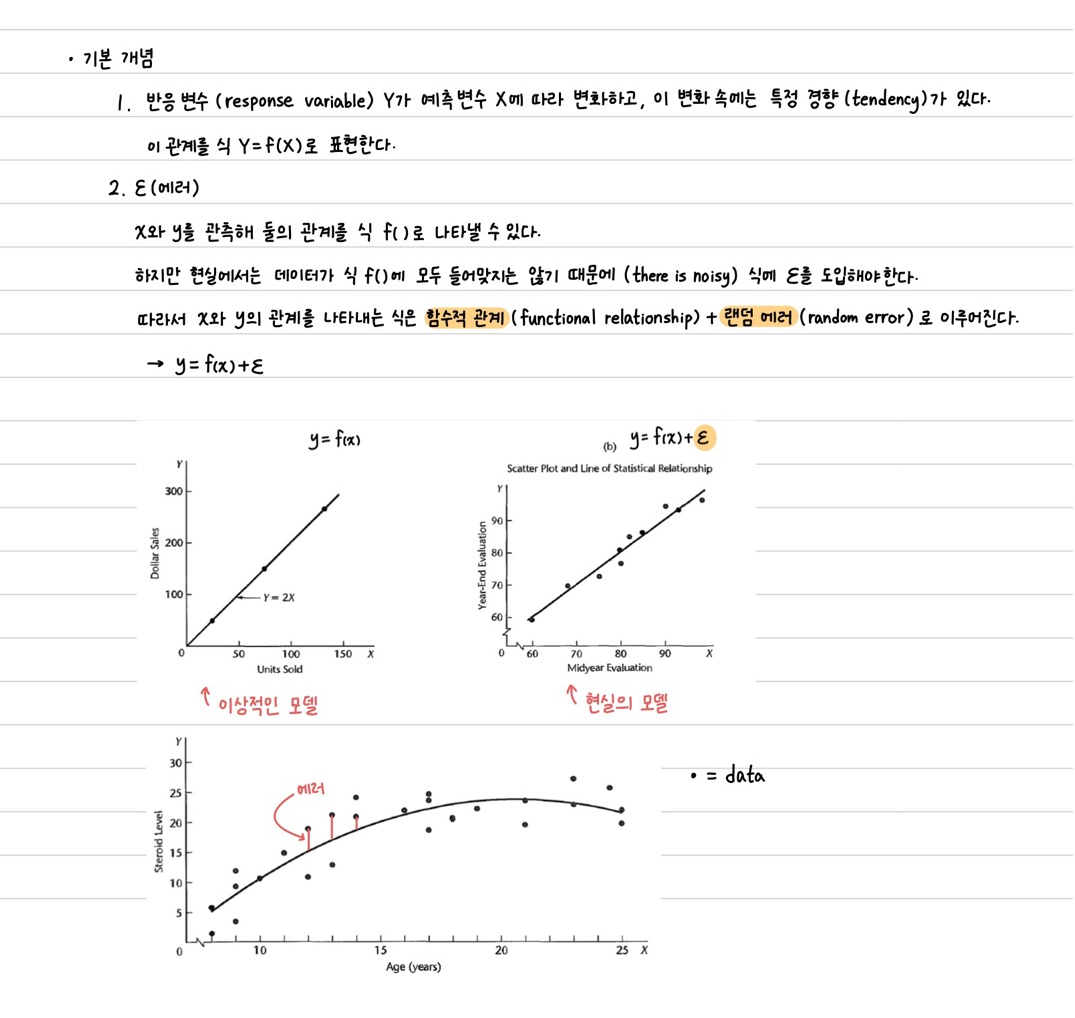
예제를 통해 위 개념들을 확인하자. 필요한 bid의 개수를 X, bid를 준비하는데 걸리는 시간을 Y라 하자.
X와 Y의 관계식 Y=9.5 + 2.1X + e를 세우고, X=45일 때의 값을 예측할 수 있다.
예측한 값은 104, 실제값은 108이므로 e는 4이다.

위 회귀 식 (Regression Line)을 그래프로 표현하면 다음과 같다.
X가 한 단위 증가할 때마다 Y가 2.1씩 증가한다는 것을 알 수 있다.
단순 선형 회귀 모형 ( Simple Linear Regression Model)
회귀 모형은 다양한 형태를 갖출 수 있다.
관계를 알아내는데 사용되는 변수의 개수는 다양하고, 관계를 표현하는 식의 형태 또한 지수함수, 삼각함수, 다항함수 등 다양하다.
이 중 가장 먼저 다룰 것은 예측 변수 X와 반응 변수 Y가 각각 한개이고, 선형관계(일차함수)를 가진 모형인 단순 선형 회귀 모형 ( Simple Linear Regression Model)이다.
단순 (simple)이라는 말은 예측 변수가 한 개라는 뜻이며, 선형 (linear)이라는 뜻은 한 모수가 다른 모수에 의해 거듭제곱, 나누기, 곱셈이 되지 않는다는 뜻이다.
위 예제에서 등장했던 식이 단순 선형 회귀 모형의 예시이다.

주의: 처음부터 오차항에 대한 가정을 이해하는 것은 불가능하지만 뒷부분에서 이에 대해 증명하므로 일단은 받아들이고 넘어가는 것이 좋다.
단순 선형 회귀 모형의 특징은 다음과 같다.
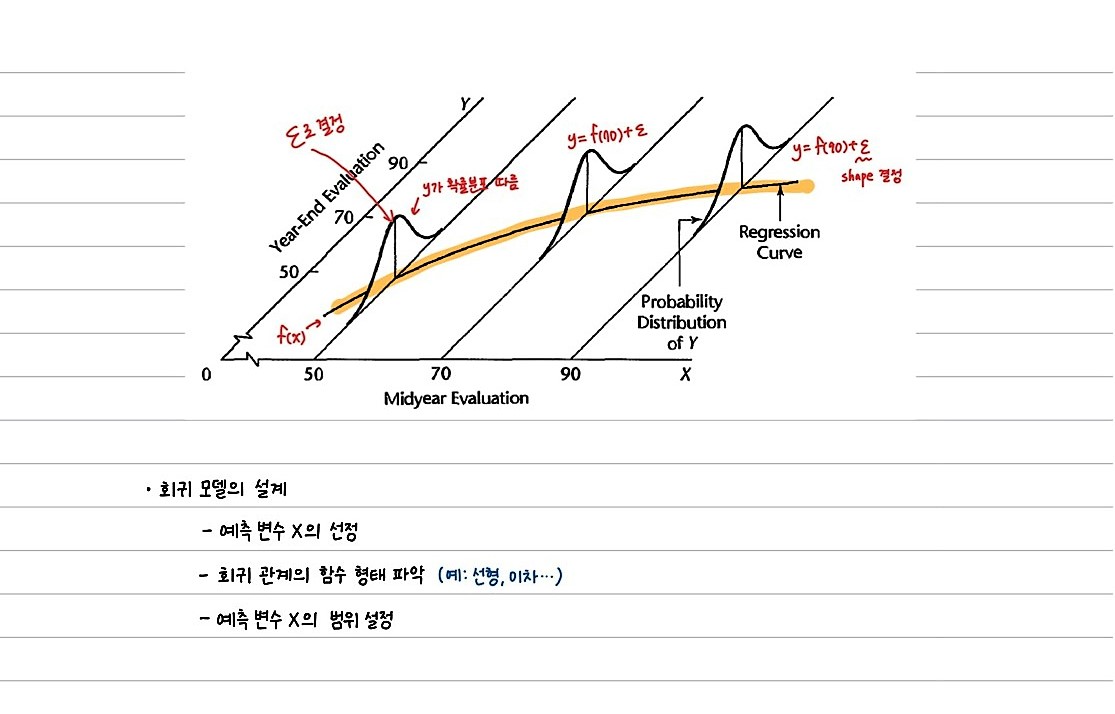
Yi의 값은 일정한 값 + 랜덤한 값으로 이루어져 있다.


아래 그래프를 보면 위 특징을 잘 이해할 수 있다.
각각의 x값에 대해 y는 특정한 분포를 갖게 되고, y=f(x)는 각 Y의 평균을 연결한 선이 된다.
'기초통계학 > 회귀 분석' 카테고리의 다른 글
| 6. 단순선형회귀에서의 추론 (Inference for Simple Linear Regression) (0) | 2023.04.02 |
|---|---|
| 5. 단순선형회귀의 변환 (Transformation of Simple Linear Regression) (2) | 2023.02.20 |
| 4. 단순선형회귀식의 진단 - 검정 (Diagnostics for a Simple Linear Model Using Test) (0) | 2023.02.16 |
| 3. 단순선형회귀식의 진단 - 그래프 (Diagnostics for a Simple Linear Model Using Graphs) (0) | 2023.02.01 |
| 2. 최소제곱법 (Least Square Method) (0) | 2022.10.04 |





댓글