단순선형회귀식의 정의와 기본적인 가정에 따르면, 회귀 모형은 몇가지 조건을 만족해야 한다.
정규오차를 가정한 단순선형회귀모형으로부터의 이탈에 관한 7개의 중요한 유형들을 검토하기 위해 잔차들을 활용하는 것을 고려해야 한다.
1. 회귀함수가 선형이 아니다.
2. 오차항의 평균이 0이 아니다.
3. 오차항이 상수분산을 갖지 않는다.
4. 오차항이 독립이 아니다.
5. 오차항은 정규분포를 따르지 않는다.
6. 모형이 하나 혹은 몇몇의 특이 관측값에 대해서는 적합하지 않다.
이번 챕터에서는 그래프를 이용해 최소제곱법으로 구한 회귀 모형이 조건들을 만족하는지 알아보자.
1. 선형성 (Linearity)
변수들 간의 관계가 전반적으로 선형 형태를 띄어야 한다. 만약 선형적 관계를 가지지 않는다면, 곡률을 줄이기 위해 값의 크기를 변화시키거나 새로운 예측 변수들을 모델에 반영해야 한다.
주어진 데이터에는 세 변수 Age, Price, Mileage가 있다. 예측 변수를 Mileage로, 반응 변수를 Price로 설정하고 회귀 모형을 구하자. 그리고 두 변수가 선형 관계를 만족시키는지 알아보기 위해 적합된 값에 대한 잔차의 그래프(Plot of residuals versus fitted values)를 구하자.
선형회귀함수가 분석된 자료에 대해 적절한지는 예측변수 대 잔차그림(redisual plot against the predictor variable) 혹은 적합값 대 잔차그림(residual plot against the fitted values)으로부터 검토할 수 있다. 회귀함수의 비선형성은 산점도(scatter plot)로 검토할 수도 있지만, 잔차그림보다 효과적이지 못하다. 이는 잔차그림이 산점도에 비해 몇 가지 중요한 이점들을 가지고 있기 때문이다. 첫째, 잔차그림은 모형의 적절성에 관한 다른 측면들을 검토하는 데 쉽게 사용될 수 있다. 둘째, 산점도의 기준 눈금이 바뀌어 관측값이 적합값에 가까이 되는 경우가 있다. 예를 들면, 기울기가 급격한 경우이다. 그러면 산점도를 이용하려 선형회귀함수의 적절성을 검토하는 것은 매우 어려워진다. 반면에 잔차그림은 이러한 조건들하에서도 적합 회귀선 근처의 편차들의 어떠한 대칭 패턴도 명확하게 보여줄 수 있다.
#데이터 불러오기
data5 <- read.csv(file="C:/Temp/eg01-05Accord.csv")
model <- lm(Price ~ Mileage , data=data5)
#그래프 그리기
with(plot(model$fitted.values,model$residuals,pch=16,xlab="Fitted Value",ylab="Residual"),data=data5)
abline(h=0,col="red")

대부분의 점들이 y=0 아래와 위에서 고르게 분포되어 있음을 알 수 있다. 이를 통해 이 회귀 모형에서 price와 mileage 변수가 충분히 둘의 관계를 설명하고 있음을 알 수 있다.

적합된 값에 대한 잔차의 그래프(Plot of residuals versus fitted values)를 그렸을 때 그래프가 위와 같이 그려진다면 회귀모형이 선형성을 만족하지 못하는 것이다.
다음은 잔차(residuals)와 오차(error)의 분포에 관한 조건들이다.
2. 평균이 0이다 (Zero Mean)
오차(error)가 0에 대해 대칭으로 분포해야 한다.
1번과 같은 데이터를 사용해 잔차에 관한 히스토그램을 그리자.
#히스토그램 그리기
hist(model$residuals,breaks=seq(-7,7,by=2),xlab="Residual", main="Histogram of residuals")
잔차(residual)이 0을 중심으로 양쪽에 분포해있음을 알 수 있다. 따라서 회귀 모형이 조건을 만족한다는 결론을 내릴 수 있다.
3. 등분산 (Constant Variance)
예측변수(X)의 변화에 따라 오차의 분산이 변하지 않는다.
1번과 같은 데이터를 사용해 실제 값과 예측된 회귀 모형을 그래프로 나타내자.
#그래프 그리기
with(plot(Mileage,Price,pch=16), data=data5)
lines(data5$Mileage, model$fitted.values,col=2,lwd=2)
최소제곱법을 이용해 추정한 직선을 그렸을 때, 각 점들이 비슷한 거리만큼 직선으로부터 떨어져있고 고르게 분포하고 있음을 알 수 있다. 따라서 회귀 모형이 등분산 조건을 만족한다고 볼 수 있다.
선형성을 파악하기 위해 그렸던 적합된 값에 대한 잔차의 그래프(Plot of residuals versus fitted values)를 사용할 수도 있다.
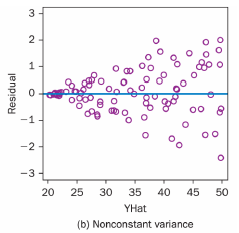
적합된 값에 대한 잔차의 그래프(Plot of residuals versus fitted values)를 그렸을 때 그래프가 위와 같이 그려진다면 회귀모형이 등분산성을 만족하지 못하는 것이다. (단, 잔차들이 y=0 직선의 위 아래로 동등하게 분포해 있기 때문에 선형성은 만족한다.)
4. 독립성 (Independence)과 무작위성 (Randomness)
오차(error)는 서로 독립이라고 가정한다. 따라서 한 점이 다른 점의 위치에 영향을 미치지 않는다. 이는 실험이 행해진 상황과 데이터가 수집된 방식을 파악해 파악한다. 예를 들어, 위 데이터에서 한 차량 판매원이 다른 판매원이 판매하는 가격에 영향을 미치지 않는다면 이 조건은 만족되는 것이다. 또한, 같은 시간대에 같은 지점에서 무작위로 표본을 수집해야 한다.
시간 순서나 혹은 다른 순서, 예를 들면 지리적으로 가까운 지역들의 순서로 자료를 얻을 때마다 순차 잔차그림(sequence plot of residuals)을 준비하는 것 또한 좋은 생각이다. 시간이나 혹은 다른 종류의 순서에 대해 잔차들을 그리는 목적은 해당 순서상에서 가까운 오차항들 간에 어떠한 상관관계가 있는지 확인하기 위해서이다.
<비독립성을 보여주는 경우>

위와 같은 잔차그림은 선형적인 시간 관련 추세 효과를 보여준다.
<독립성을 보여주는 경우>
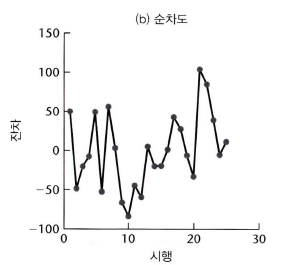
오차항이 독립일 때는 위 그래프와 같이 순차도의 잔차들이 기준선 0 근처에서 확률적 패턴으로 변동한다.
5. 정규성 (Normality)
오차(error)가 정규 확률 분포를 따른다고 가정한다.
잔차(residual)에 관한 Q-Q plot (Normal Quantile Plot)을 그래프로 그리자.
잔차의 정규확률그림 (normal probability plot of the residual or normal quantile plot)에서 각각의 잔차들은 정규성하의 기댓값과 대응하여 그래프에 좌표가 찍힌다. 직선과 가까운 형태가 정규성을 보이는 것이며 직선으로부터 상당히 벗어난 그림은 오차분포가 정규분포를 따르지 않는다는 것을 의미한다.
#그래프 그리기
qqnorm(model$resid,pch=16)
qqline(model$resid,col="red",lwd=2)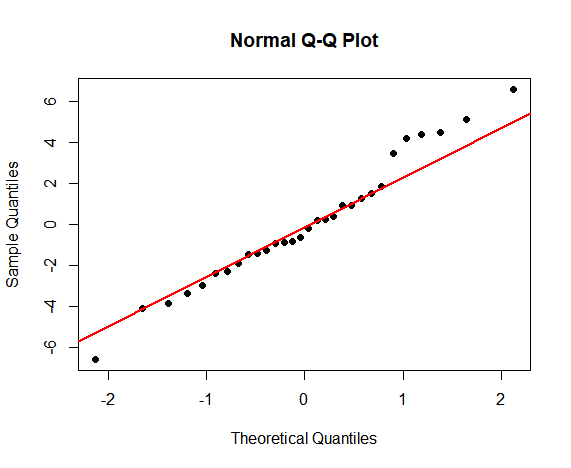
그래프의 우측에 위치한 몇몇의 점들을 제외하고는 직선의 형태를 상당히 일정하게 따른다는 것을 보여주므로, 회귀 모형이 정규성을 만족함을 알 수 있다.
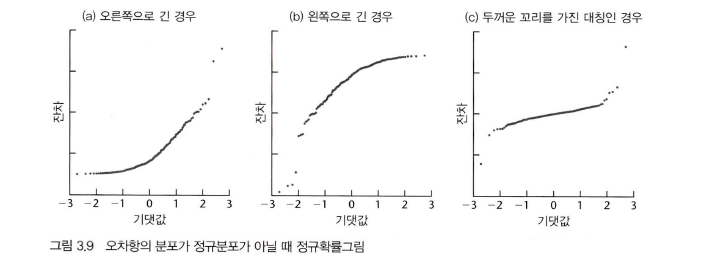
적합된 값에 대한 정규확률그림(Plot of residuals versus fitted values)를 그렸을 때 그래프가 위와 같이 그려진다면 오차항의 분포가 정규성으로부터 심각하게 이탈한다는 것을 의미한다.
6. 특이점의 존재
특이점은 극단적인 관측값이다. 잔차 특이점은 잔차의 상자그림(box plots), 줄기-잎 그림(stem-and-leaf plots), 점그림(dot plots)뿐만 아니라 X 또는 적합값에 대한 잔차그림(residual plots against X or fitted values)으로부터 찾아낼 수 있다.
<특이점에 대한 자세한 글>
특이점은 문제를 유발할 수 있다. 특이점이 나왔을 때 우선 확인해야 될 것은 그 관측값이 실수나 혹은 다른 특단적인 효과로부터 기인한 것인지, 그래서 제거되어야 하는 것인지에 대한 것이다. 이 특이점을 제거하는 주요한 이유는 최소제곱법에 대한 적합선이 특이점을 향해 불균형적으로 끌어당겨지기 때문이다. 만약 특이 관측값이 정말로 실수나 다른 극단적인 원인으로부터 생긴 것이라면, 이러한 현상은 잘못된 적합을 만든다. 반면에 모형에 반영되지 않은 다른 예측변수들과의 상호작용 때문에 발생한 특이점의 경우에는 유의미한 정보를 전달할 수도 있다. 가장 많이 제안되는 안전한 방법으로는 특이점이 기록에서의 오류, 잘못된 계산, 장비의 오작동 혹은 유사한 상황들을 나타낸다는 직접적인 증거가 있을 경우에만 특이점들을 제거하는 것이다.
잔차에 관한 상자그림(box plot)을 그리자.
#상자그림 그리기
boxplot(model$residuals)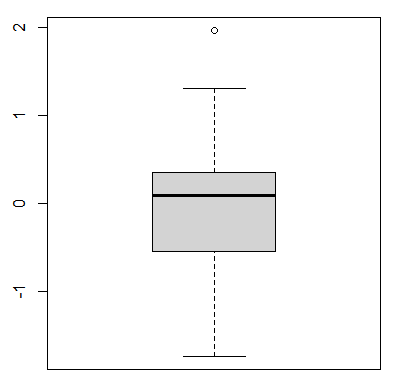
잔차에 대한 상자그림을 그렸을 때 특이점(outlier)이 한 개 있다는 것을 알 수 있다.
'기초통계학 > 회귀 분석' 카테고리의 다른 글
| 6. 단순선형회귀에서의 추론 (Inference for Simple Linear Regression) (0) | 2023.04.02 |
|---|---|
| 5. 단순선형회귀의 변환 (Transformation of Simple Linear Regression) (2) | 2023.02.20 |
| 4. 단순선형회귀식의 진단 - 검정 (Diagnostics for a Simple Linear Model Using Test) (0) | 2023.02.16 |
| 2. 최소제곱법 (Least Square Method) (0) | 2022.10.04 |
| 1. 선형 단순 회귀 모형 (Linear Simple Regression Model) (0) | 2022.10.02 |





댓글