데이터를 이용한 예제를 통해 단순선형회귀에서의 추론을 진행해보자.
먼저 데이터를 불러오자.
#데이터 불러오기
install.packages("Stat2Data")
library(Stat2Data)
data("Sparrows")
Sparrows
참새에 관한 데이터인 "Sparrows"에는 범주형 변수 Treatment와 연속형 변수 Weight, Winglength가 있음을 알 수 있다.
참새의 몸무게인 Weight와 참새의 날개 길이인 Wing Length 사이에 존재하는 관계를 찾아내기 위해 회귀 모형을 만들자.
model <- lm(WingLength ~ Weight, data=Sparrows)
model

회귀모형은 다음과 같다.

위 회귀모형에 대해 추론하기 전에 그래프를 통해 회귀모형이 데이터를 설명하기에 적합한지 검토해보자.
#데이터를 표현한 산점도 위에 회귀모형 나타내기
with(plot(WingLength, Weight), data=Sparrows)
lines(Sparrows$WingLength, model$fitted, col="red", lwd=2)
그래프를 통해 회귀모형이 적합함을 알 수 있다.
이번에는 가설검정과 신뢰구간을 통해 회귀모형에 대해 추론해보자.

회귀 함수 직선과 실제 데이터를 표현한 점들과의 거리가 가깝고 이상점이 많지 않으므로 이 모형이 데이터를 충분히 설명한다고 결론내릴 수 있다.
1. 기울기(회귀 계수)에 대한 가설 검정
회귀 모형의 기울기(B1)에 대한 추론에 관심이 있다고 하자. B1=0인지 아닌지 검정하는 데 관심이 있는 이유는 B1=0일 때, Y와 X의 선형관계가 존재하지 않기 때문이다. 일반적으로 X와 Y 사이에 선형관계가 있는지 가장 먼저 확인하므로, 기울기에 대한 가설 검정을 먼저 해보는 것이 좋다.

위에서 불러왔던 "Sparrows"라는 데이터에서 예측변수 X인 날개 길이(wing length)와 반응변수 Y인 몸무게(weight) 간의 관계를 나타내는 기울기에 관한 회귀 계수 B1을 검정하자.

summary(model)
B1의 p-value의 값이 0에 가까우므로, 귀무가설을 기각하고 대립가설을 채택할 수 있다. (B1의 값은 0이 아니다.)
따라서 회귀 계수인 B1의 값은 0이 아니며, Y와 X 간 선형관계가 존재한다는 것을 알 수 있다.
"anova" 함수를 이용해도 같은 결과를 얻을 수 있다.

B1의 p-value의 값이 0에 가까우므로, 귀무가설을 기각하고 대립가설을 채택할 수 있다는 같은 결론(B1의 값은 0이 아니다)을 얻을 수 있다.
2. 기울기(회귀 계수)에 대한 신뢰 구간
단순선형회귀식이 다음과 같을 때,
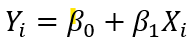
X와 Y 간의 관계를 나타내는 회귀 모형의 기울기(회귀 계수 B1)에 대한 신뢰구간을 구할 수 있다.

위에서 불러왔던 "Sparrows"라는 데이터를 적합시킨 회귀 모형의 회귀 계수 B1에 대한 95% 신뢰구간을 구하자.
summ <- summary(model)
c("lower" = summ$coef[2,1] - qt(0.975, df = summ$df[2]) * summ$coef[2, 2],
"upper" = summ$coef[2,1] + qt(0.975, df = summ$df[2]) * summ$coef[2, 2])
위 데이터에서 회귀 모형의 기울기에 대한 95% 신뢰 구간은 (0.399, 0.536)임을 알 수 있다.
혹은 "confint"라는 함수를 이용해 간단하게 구할 수 있다.
confint(model)
위에서 사용했던 코드와 같은 결과를 얻음을 알 수 있다.
3. 결정 계수(coefficient of determination)에 대한 추론
summary(model)$r.squared

결정계수는 모형에 의해 설명될 수 있는 반응 변수를 분수로 나타낸 값으로, Y 변수 (참새의 몸무게)의 61.4%가 날개 길이를 바탕으로 한 선형 회귀 모형에 의해 설명될 수 있음을 의미한다.
4. 상관관계(correlation)에 대한 추론
cor(Sparrows$WingLength, Sparrows$Weight)

상관관계의 값이 0.784이므로, 참새의 몸무게와 날개 길이 사이에는 강한 양의 관계가 존재함을 알 수 있다.
'기초통계학 > 회귀 분석' 카테고리의 다른 글
| 5. 단순선형회귀의 변환 (Transformation of Simple Linear Regression) (2) | 2023.02.20 |
|---|---|
| 4. 단순선형회귀식의 진단 - 검정 (Diagnostics for a Simple Linear Model Using Test) (0) | 2023.02.16 |
| 3. 단순선형회귀식의 진단 - 그래프 (Diagnostics for a Simple Linear Model Using Graphs) (0) | 2023.02.01 |
| 2. 최소제곱법 (Least Square Method) (0) | 2022.10.04 |
| 1. 선형 단순 회귀 모형 (Linear Simple Regression Model) (0) | 2022.10.02 |





댓글