이번 시간에는 벡터의 내적에 대해 알아보자.
벡터의 내적은 벡터끼리 곱해 스칼라 값이 결과로 나오게 하는 계산이다.
벡터의 내적은 주로 아래의 두가지 식을 사용해 값을 구한다.
1. u∙v=|u||v|cosθ
2. u∙v=u1v1+u2v2+u3v3
내적의 결괏값은 항상 스칼라값으로 표현된다는 점을 주의하자.

내적의 값을 구하는 공식인 u∙v=|u||v|cosθ를 제2코사인법칙을 이용해 증명해보자.

내적은 벡터 사이의 각을 구할 때 매우 유용하다.
벡터의 내적을 이용해 두 백터의 사잇각을 구하는 예제를 풀어보자.

벡터의 내적이 어떻게 과학이나 공학에서 활용되는지 와닿지 않을 수 있다.
직관적이면서도 간단한 벡터의 내적 활용 예시로는 가중치 평균이 있다.


이번에는 내적을 이용해 벡터의 상대적 유사성을 측정해보자.
여기서 벡터의 유사성이란 "얼마나 비슷한 방향을 향하고 있는가"를 의미한다.
두 벡터가 비슷한 방향으로 향할수록 두 벡터의 사잇각 θ가 작아지고, cosθ의 값은 커지며, 내적의 값은 커진다.
따라서 두 벡터가 비슷한 방향으로 향할수록 내적의 크기가 크다.


벡터의 내적에도 코시-슈바르츠 부등식을 적용할 수 있다.

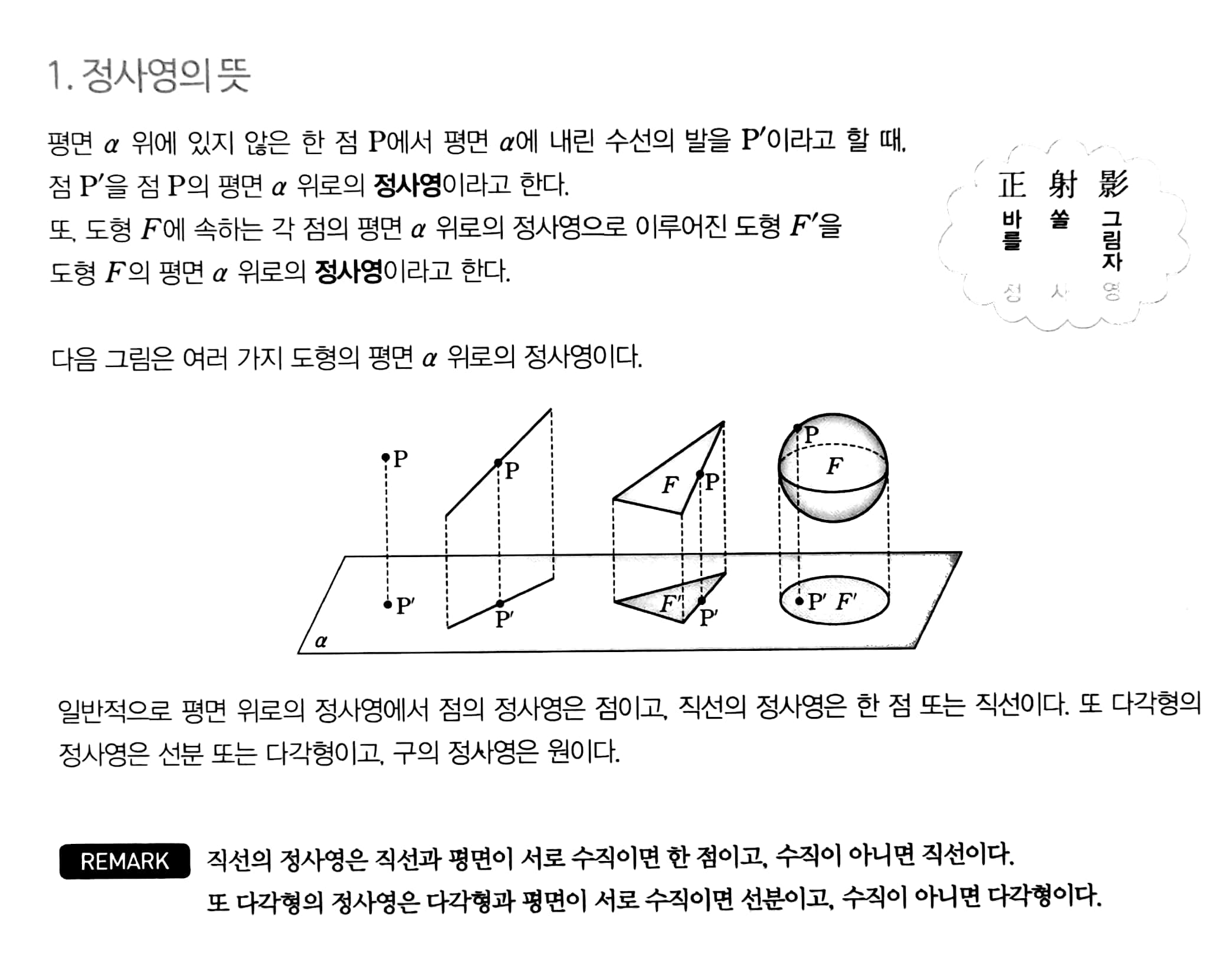
마지막으로, "정사영"이라는 개념이 등장하는데 정사영의 영어 표현인 "orthogonal projection"이라는 말에서 이해할 수 있듯이 점,직선, 도형 위에서 빛을 비췄을 때 생기는 그림자의 모양을 정사영이라고 생각하면 된다.
빛을 비추는 평면 위로 수선의 발을 내려 그리면 정사영이 완성된다
(아래 그림은 고등학생 때 기하와 벡터를 공부하며 사용했던 책에서 가져왔다. 역시 고등학교 교재가 짱이다..)
이제 정사영을 벡터에 적용해보자.
정사영의 길이와 벡터를 구하는 식과 유도되는 과정을 꼭 알아두자.

이번 시간에는 벡터의 내적에 대해 알아보았고, 내적을 활용한 사잇각 구하기, 벡터의 유사성 측정, 정사영 구하기를 해보았다.
개인적으로는 벡터의 내적을 계산할 때 어떤 값이 벡터값이고 어떤 값이 스칼라값인지 잘 구분하고 혼동하지 않도록 주의해야 한다고 생각한다. 언제나 벡터값과 스칼라값을 잘 구분하는 것이 중요하다.
'기초통계학 > 선형대수학' 카테고리의 다른 글
| 15. 벡터 공간 (Vector Space) (0) | 2022.05.30 |
|---|---|
| 13. 벡터 (Vector) 기초 (0) | 2022.05.28 |
| 12. 가우스 소거법을 이용한 역행렬의 계산 (Calculation of Inverse Matrix Using Gaussian Elimination) (0) | 2022.05.28 |
| 11. 가우스 소거법 (Gaussian Elimination) (0) | 2022.05.25 |
| 10. 크래머의 법칙(Cramer's Rule) (0) | 2022.05.23 |





댓글